After creating a system model as shown on the system modeling page, I used Matlab to transform The EOM's of the plate and ball system into state space form x_dot = Ax + Bu, where x is the state vector and u is the input vector.

The Matlab code can be acsessed here: https://bitbucket.org/ebriefer/me305_lab/src/master/ME405/ME405_HW04.mlx
To verify my model, I ran simulations in matlab with the system at equilibrium (ball centered on horizontal plate), with the ball initially 5cm off center from the plate, and with a closed loop full state regulator to attempt to return the system to equilibrium. The results of these simulations are shown below.

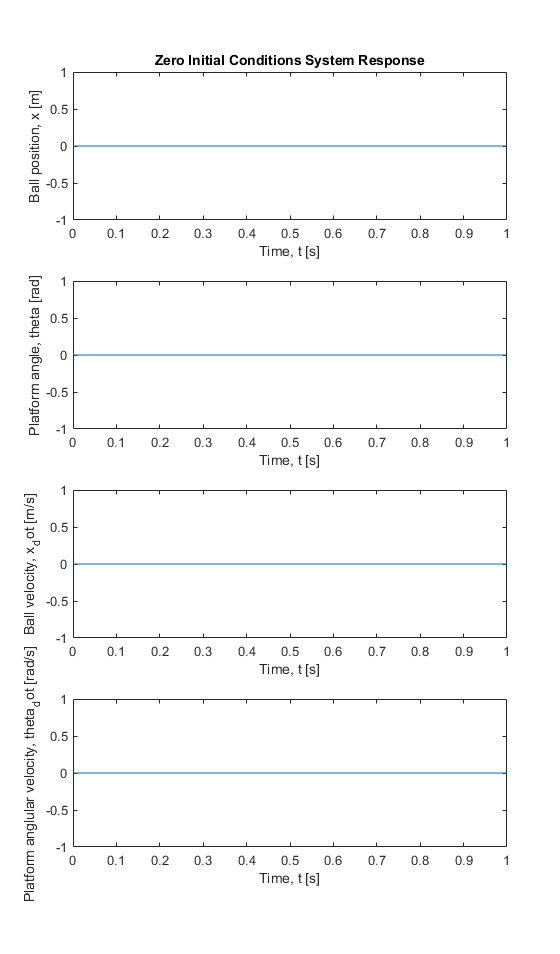
Starting at equilibrium with no input torque the system remains at equilibrium as I would expect.

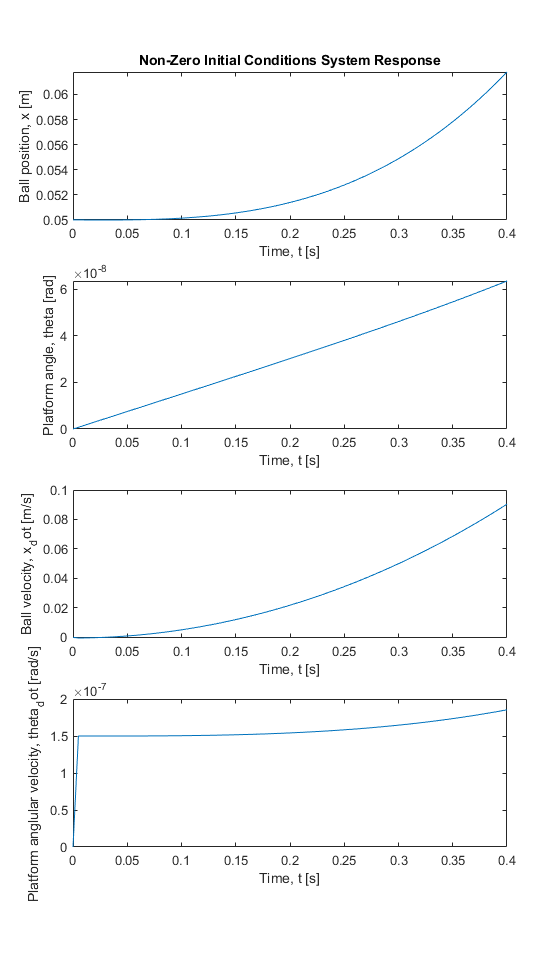
Starting with the ball displaced 5cm from the center of the plate the ball accelerates away from the center of the plate and the plate begins to rotate down. In general, this is the response I would expect from this system, since it is unstable. However, the initial sharp jump in platform velocity is not what I would expect given that the platform has mass and is starting from rest. This may indicate that there is a problem in my equations of motion.

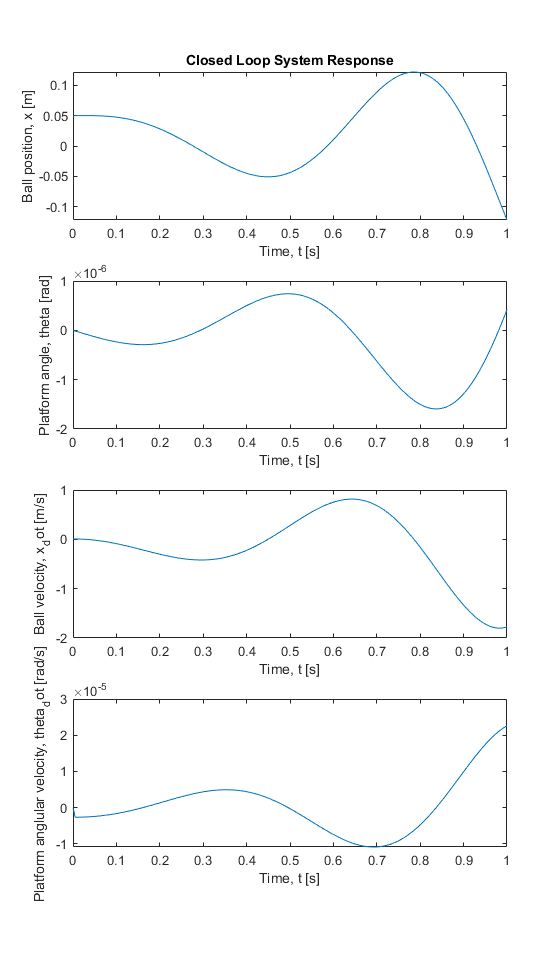
With a full state regulator added to the system to attempt to stabalize it, the system now oscillates around the equilibrium point. However, the system is still unstable as the amplitude of the oscilation of both the balls position and the plate angle increases over time. This further indicates that there is a problem with the equations of motion.